Q. 정렬 알고리즘에 대해 설명해주세요.
글 작성자: 택시 운전사
반응형
Q. 정렬 알고리즘에 대해 설명해주세요.
Goal
- 정렬 알고리즘의 개념을 설명할 수 있다.
- 정렬 알고리즘의 종류에 대해 설명할 수 있다.
정렬 알고리즘의 개념
정렬 알고리즘이란
- 데이터들이 주어졌을 때 이를 정해진 순서대로 나열하는 것
- 얼마나 효과적으로 해결하는 지가 정렬 알고리즘의 핵심
정렬 알고리즘이 중요한 이유
- 데이터가 정렬되어 있으면 이진탐색이라는 강력한 알고리즘을 사용할 수 있다.
대표적인 정렬의 종류
- 실제 응용에서는 상황에 따라 두 가지 이상의 정렬 방법을 사용하는 경우가 많다.
- 정렬 대상이 특정 크기 이하로 단편화될 때까지는 퀵 정렬을 쓰다가, 삽입정렬을 쓴다던가, 특정 횟수 이상 재귀호출이 발생하면 O(nlgn)의
힙 정렬을 사용한다.
버블정렬(Bubble Sort)
방법
1번째와 2 번째 원소를 비교하여 정렬하고, 2번째와 3번째, ... , n-1번째와 n번째를 비교하여 정렬한 뒤 다시 처음으로 돌아가 이번에는 n-2번째 와 n-1번째까지해서 총 n(n-1)/2 번 정렬한다.
시간복잡도
- 가장 쉬운 정렬 알고리즘이지만, 거의 모든 상황에서 최악의 성능을 보여준다
예시
def BubbleSort(li):
len_list = len(li)
# 두 개씩 비교하기 때문에 범위는 `range(len_list-1)`이 되어야 한다.
for i in range(len_list-1):
# 안 쪽의 `for loop`는 실제 비교를 하는 부분에 해당한다.
# 따라서 범위는 `range(len_list-i-1)이 되어야 한다.
# 1번째와 2 번째 원소를 비교하여 정렬하고, 2번째와 3번째, ... , n-i-1번째와 n-i번째를 비교하여 정렬한다.
for j in range(len_list-i-1):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
return li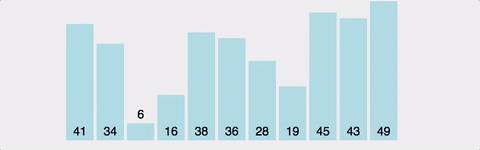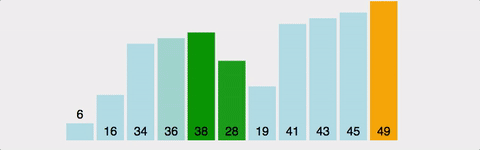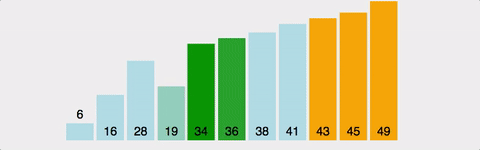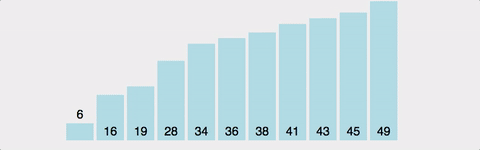
선택정렬(Selection Sort)
방법
1번째부터 끝까지 훑어서 가장 작은 것을 찾아서 1번째에, 2번째부터 끝까지 훑어서 가장 작은 것을 찾아서 2번째에 ... (n-1)번을 반복한다.
- 주어진 리스트 중에 최솟값을 찾는다.
- 그 값을 맨 앞에 위치한 값과 교체한다.
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
시간복잡도
예시
def selection_sort(li):
for i in range(len(li)-1):
min_idx = i
for j in range(i+1, len(li)):
if li[min_idx] > li[j]:
min_idx = j
if min_idx != i:
li[i], li[min_idx] = li[min_idx], li[i]
return li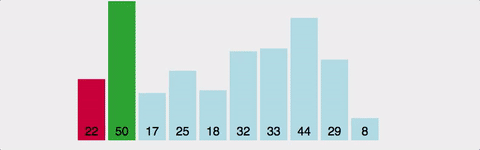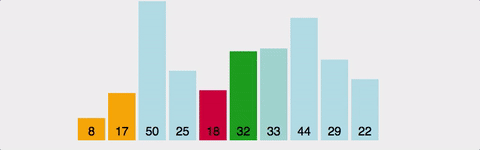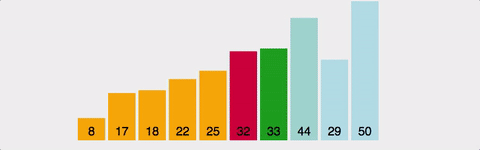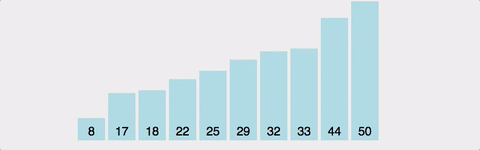
삽입정렬(Insertion Sort)
방법
1부터 n까지 Index를 설정하여 현재 위치보다 아래쪽을 순회하며 현재 위치의 값을 현재 위치보다 아래쪽으로 순회하며 알맞은 위치에 넣어주는 알고리즘이다.
시간복잡도
예시
def insertion_sort(li):
for i in range(1, len(li)):
j = i - 1
key = li[i]
while li[j] > key and j >= 0:
li[j+1] = li[j]
j -= 1
li[j+1] = key
return li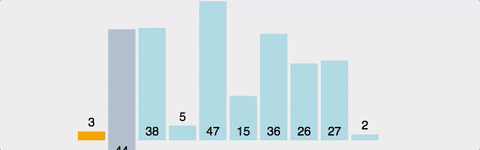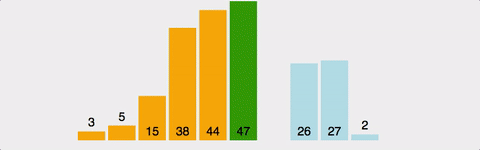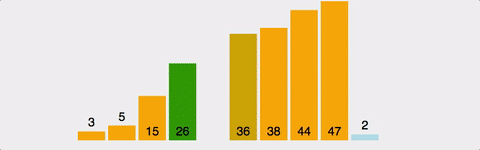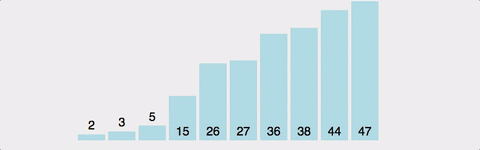
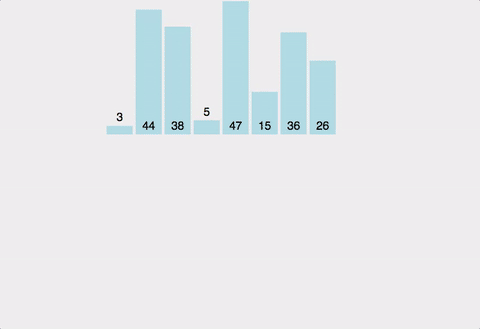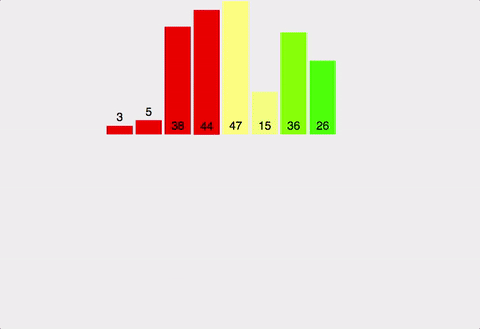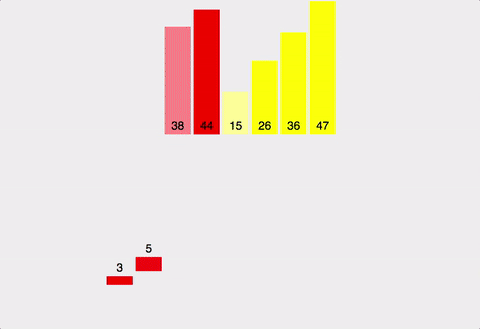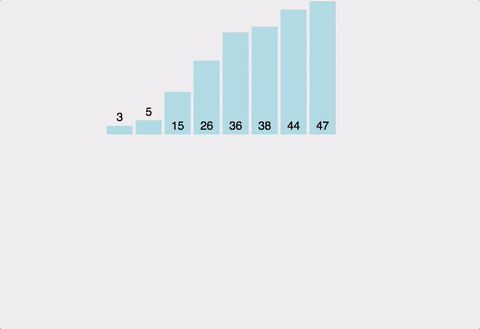
병합정렬(Merge Sort)
방법
리스트를 반으로 쪼개나가며 좌측과 우측 리스트를 계속 하여 분할해 나간 후 각 리스트 내에서 정렬 후 병합 정렬 후 병합하는 과정을 통해 정렬하는 알고리즘
시간복잡도
- 가장 많이 쓰이는 정렬 알고리즘 중 하나
예시
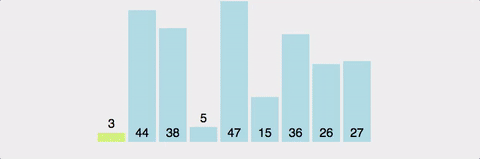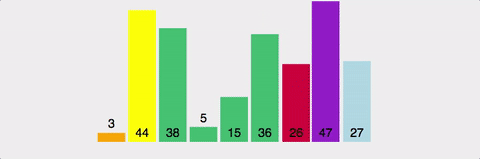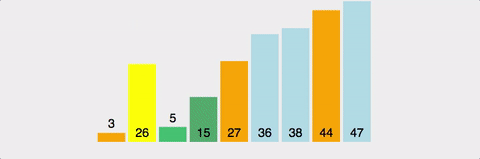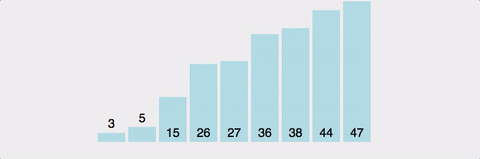
퀵정렬(Quick Sort)
방법
pivot을 선정하여 pivot을 기준으로 좌측과 우측으로 pivot보다 작은 값은 왼쪽에 pivot보다 큰 값은 오른쪽으로 재배치하고 계속하여 분할하여 정렬하는 알고리즘
시간복잡도
- 최악의 경우 ( pivot이 최대 혹은 최소인 경우 )
- 일반적인 경우
- 이름 그대로 real-world 데이터에서 빠르다고 알려져 있어 가장 많이 쓰는 정렬 알고리즘
- pivot은 랜덤으로 잡거나, 3개나 9개 원소를 골라서 중앙값을 선택한다.
예시
반응형
'Algorithm > Problem Solving' 카테고리의 다른 글
| [BOJ] 👸 N-Queens / 파이썬 (3) | 2019.02.01 |
|---|---|
| [프로그래머스] 🚍 셔틀버스 - [1차] 2018 카카오 블라인드 채용 / Python / KAKAO BLIND RECRUITMENT (0) | 2019.02.01 |
| [프로그래머스] 이상한 문자 만들기 / 파이썬 (0) | 2019.01.31 |
| [프로그래머스] 👨🎓 N으로 표현 / 파이썬 (0) | 2019.01.31 |
| [프로그래머스] 🔐 시저 암호 / 파이썬 (0) | 2019.01.31 |
댓글
이 글 공유하기
다른 글
-
[프로그래머스] 🚍 셔틀버스 - [1차] 2018 카카오 블라인드 채용 / Python / KAKAO BLIND RECRUITMENT
[프로그래머스] 🚍 셔틀버스 - [1차] 2018 카카오 블라인드 채용 / Python / KAKAO BLIND RECRUITMENT
2019.02.01 -
[프로그래머스] 이상한 문자 만들기 / 파이썬
[프로그래머스] 이상한 문자 만들기 / 파이썬
2019.01.31 -
[프로그래머스] 👨🎓 N으로 표현 / 파이썬
[프로그래머스] 👨🎓 N으로 표현 / 파이썬
2019.01.31 -
[프로그래머스] 🔐 시저 암호 / 파이썬
[프로그래머스] 🔐 시저 암호 / 파이썬
2019.01.31

